Graphe de Gosset
| Graphe de Gosset | |
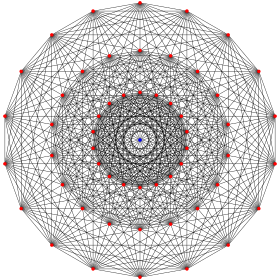 Représentation du graphe de Gosset. Deux sommets se superposent au centre de cette représentation (ainsi que les arêtes adjacentes aux sommets centraux). | |
| Nombre de sommets | 56 |
|---|---|
| Nombre d'arêtes | 756 |
| Distribution des degrés | 27-régulier |
| Rayon | 3 |
| Diamètre | 3 |
| Maille | 3 |
| Automorphismes | 2 903 040 |
| Propriétés | Graphe de Taylor Distance-régulier Intégral Hamiltonien |
| modifier |
|
Le graphe de Gosset est, en théorie des graphes, un graphe 27-régulier possédant 56 sommets et 756 arêtes.
Propriétés[modifier | modifier le code]
Propriétés générales[modifier | modifier le code]
Le diamètre du graphe de Gosset, l'excentricité maximale de ses sommets, est 3, son rayon, l'excentricité minimale de ses sommets, est 3 et sa maille, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 27-sommet-connexe et d'un graphe 27-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 27 sommets ou de 27 arêtes.
Le graphe de Gosset est localement le graphe de Schläfli, c'est-à-dire que quel que soit le sommet s considéré, le sous-graphe induit par les 27 voisins de s est isomorphe au graphe de Schläfli.
Propriétés algébriques[modifier | modifier le code]
Le groupe d'automorphismes du graphe de Gosset est un groupe d'ordre 2 903 040. Il est isomorphe au groupe de Lie E7, le groupe d'isométrie d'une variété riemannienne de dimension 64 appelée plan projectif quateroctionique.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Gosset est : . Il n'admet que des racines entières. Le graphe de Gosset est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.
Voir aussi[modifier | modifier le code]
Liens internes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- (en) Eric W. Weisstein, Gosset Graph (MathWorld)

